A way of expressing very large or very small number using power of 10.
coefficient = a, base = 10, exponent = b
Write a number in scientific notation:
Example:
1) 125,000,000,000
a) Put a decimal after the first digit and drop the zeros; 1.25 will be the coefficient
b) To find the exponent, count the places from the decimal to the end of the number; 11 is the exponent
c) So, the scientific notation is 1.25 x 10 ^11
2) 0.000000000000244 = 2.44 x 10^-13
(Numbers smaller than 1 will have a negative exponent)
3) 360,000,000,000,000 = 3.6 x 10^14
4) 0.000000297 = 2.97 x 10^-7
5) 125,000,000 = 1.25 x 10^8
6) 1,380,000 = 1.38 x 10^6
7) .000,006 = 6.0 x 10^-6
8) .0000274 = 2.74 x 10^-5
Adding and Subtract using Scientific Notation:
Examples:
1) 3.6 x 10^5 2) 8.4 x 10^8
+ -
4.5 x 10^5 3.2 x 10^8
------------- -------------
8.1 x 10^5 5.2 x 10^8
3) 4.5 x 10^6 => 0.45 x 10^7
+
2.2 x 10^7 2.2 x 10^7
^ --------------
|| 2.65 x 10^7
||
a) increase the smaller exponent to equal the larger exponent
b) decrease the size of corresponding coefficient amount
4) 3.3 x 10^9 3.3 x 10^9
+ => +
2.2 x 10^8 0.22 x 10^9
--------------
3.52 x 10^9
5) 8.4 x 10^5 8.40 x 10^5
- => -
3.4 x 10^4 0.34 x 10^5
-------------
8.06 x 10^5
6) 3.3 x 10^-7 3.30 x 10^-7
+ => +
8.6 x 10^-8 0.86 x 10^-7
---------------
4.16 x 10^-7
7) 3.6 x 10^-9 3.60 x 10^-9
- => -
4.4 x 10^-10 0.44 x 10^-9
----------------
3.16 x 10^-9
Multiply and Divide using Scientific Notation:
A) When multiply, multiple the coefficients with the powers of ten, you add the exponent.
(a x 10^b) * (c x 10^d) = (a*c) x 10^(b +d)
Example 1:
(5.2 x 10^2) * (2.5 x 10^3) = (5.2*2.5) x 10^(2+3) = 13 x 10^5 (Proper scientific notation is 1.3 x 10^6)
B) When divide, divide the coefficient with the powers of ten, you subtract the exponent.
(a x 10^b) / (c x 10^d) = (a/c) x 10^(b-d)
Example 1:
(6.3 x 10^4) / (2.1 x 10^2) = 6.3/2.1 x 10^(4-2) = 3 x 10^2
Example 2:
(8.49 x 10^-6) / (3.0 x 10^-3) = (8.49/3.0) x 10^(-6-( -3)) = 2.83 x 10^ -3 (Negative exponent!)
Example 3:
(8 x 10^3) (2 x 10^2)
------------------------- = [(8)(2)] /4 x 10^[ (3+2)-3] = 4 x 10^2
(4 x 10^3)
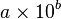
No comments:
Post a Comment