Graphical Analysis of Motion

Graphical Analysis of Motion

     Distance vs Time or Displacement vs Time or Position vs Time

• The slope always represent the speed on a distance vs time graph.
• High slope = faster speed
• Low slope = slower speed
• A straight line  means constant speed
• slope = rise/ run = 5/2 = 2.5 m/s = constant speed
• slope = 5 m/ 2 s = 2.5 m/s

Example: 

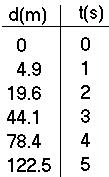
     If a rock is dropped from a high cliff. The rock fall for 5 sec, how far did it traveled?

     

d = si*t + (1/2)a t^2     si = 0 (initial speed)    t = 5s    a = 9.8 m/s^2

d1 = 1/2 (9.8) (1s)^2 = 4.9 m

d2 = 1/2 (9.8) (2s)^2 = 19.6 m

d3 = 1/2 (9.8) (3s)^2 = 44.1 m

d4 = 1/2 (9.8) (4s)^2 = 78.4 m

d5 = 1/2 (9.8) (5s)^2 = 122.5 m

    

   

• A constant acceleration will create a curve line (parabola).
• The slope at any given point is the speed or velocity at that instant
• The instantaneous speed is found by drawing a tangent line to any point on the curve line.
• slope = Δd / Δt 

 Speed vs Time graph

• Area below the line on a speed vs time graph is the distance traveled.
• Area = L * W => d = s * t =  3 s * 10 m/s = 30 m

• Straight line means constant acceleration = slope = (6 m/s) / 5 s = 1.2 m/s^2
• Initial speed =0, Distance traveled =>d = (1/2)at^2 = (1/2) (1.2)(5)^2 = 15 m
• Area = 1/2bh = (1/2)(5)(6) = 15 m 

Velocity vs Time graph

• Slope is always = accelerate on a velocity vs time graph
• In this case the slope is negative, so it is decelerate.
• Slope = (0-140)/ (8-0) = - 17.5 m/s^2
• Distance = Area of the line => A = (1/2)bh = (1/2)(8)(140) = 560 m
• Distance = d = si*t + (1/2) at^2 = (140)(8) + (1/2) (-17.5) (8)^2 = 560 m

Acceleration vs Time graph

• Straight line means constant acceleration = 10 m/s^2 , but velocity is changing by the same rate each second
• Area under the line gives the change in velocity during the time interval 5 secs. 

Area = (10 m/s^2 )(5s) = 50 m/s =  Δv (change in velocity)

Formula:

1) d = si*t = (1/2) a*t^2     a = (2d) / t^2

2) d = (sf^2 - si^2) / 2a     a = (sf^2 - si^2) / 2d

3) a = (sf - si) / t     t = (sf -si) / a

    _

4) s = d / t     t = d / s     d = s*t

    _

5) s = (si +sf) /2

6) sf = si + a*t