Friction

• Is the force which opposes the motion of two objects or surfaces that are in contact with each other
• Fore example, a box sitting on a floor. The force holding the surfaces together is called the Normal force.
• The Normal force is defined as the force which acts perpendicular to the contact surface.

                                                   Fgravity = w = Fn

• The amount of frictional force is determined by the amount of force holding the two surfaces together. It is also determined by the roughness of the two surfaces.

Identifying forces: If the box moves across the floor at a constant speed, the forces acting on it are balanced.

• Frictional force = Ff, this force oppose the motion of the box
• Normal force = Fn, this hold the contact surface together. It is perpendicular to the contact surfaces.
• Applied force = Fa, is the force moving the box across the floor.

Coefficient of friction

• Is a constant for any two surfaces in contact with each other
• It is number determined by the roughness of the surfaces.
• The rougher the surfaces are, the higher the coefficient of friction.
• It is calculated using this formula: μ = Ff / Fn
• μ (mu) is the coefficient of friction, it is unitless
• Ff is the force of friction
• Fn is the normal forces

Example: A box of 15kg being pushed forward at a constant speed. The applied force is 50 N. What is the coefficient of friction?

     Fn = w = mg = 15kg (9.8 m/s^2) = 147 N

     Ff = Fa, μ = Ff/Fn = 50 N/ 147 N = 0.34

Newton's Third Law of Motion

For every action , there is an equal and opposite reactions.

Example 1: Rocket

Example 2: Walking forward

Example 2: Sitting on a chair

-----------------------------------------

Next related topic: Friction

Newton's Second Law of Motion

• F= ma (Force = mass * acceleration)
• A force is defined as a pushed or pull
• In the metric system, force is measured in Newtons (N).
• A newton is approximately equal to 1/4 lb (pound)
• In physics, mass is usually measured in kilograms
• Acceleration is measured in m/s^2

Example 1: A rocket of mas 1750 kg fires it engines in spaces. The engine exert of force of 4500 N. 

     a) At what rate will the rocket accelerate?

     F = ma => 4500 N = 1750 kg * a, solve for a,

     a = 4500/1750 = 2.57 N/g = 2.57 m/s^2

     b) How fast will the rocket be moving at the end of 25 s?

     

     Sf = si + at => Sf= 0 + (2.57 m/s^2) (25s) = 64.25 m/s

Example 2: Two forces act on a box. One force is 500 N and acts to the right. The second force is 840 N, and act to the left.

      a) What is the net force acting on the box?

     Fnet = Fa - Ff  = 840 -500 = 340 N left

    b) If the box mass is 120 kg, at what rate does it accelerate?

     F = ma => 340 N = (120 kg) a, a = 2.83 N/kg  or m/s^2

Weight:

• Weight refers to the force of gravity acting on an object
• The formula for calculating the weight of an object is a variation of Newton's 2nd Law.
• W= mg (Weight = mass * gravitational acceleration (9.8 m/s^2))
• Remember, mass is the amount of matter contained within an object. If you shoot a heavy object into space. Its weight will disappear, but its mass will be unchanged.

Example 1: An object has a mass of 320 kg. How much does this object weight?

     

     W = mg = 320 kg (9.8 m/s^2) = 3136 N

Example 2: A man weight 850 N. What is his mass?

     W = mg => 850 N = m (9.8 m/s^2), m = 86.7 kg

Example 3: 

 a) A man stands on a scale in an elevator. The elevator is not moving. The man's mass is 75 kg. What is the reading on the scale?

     W = mg = 75(9.8) = 735 N

b) If the elevator beginning to move upward 2 m/s^2. What is the reading on the scale now?

     F = ma = 75 kg ( 2 m/s^2) = 150 N

     Fnet = 735 N + 150 N = 885 N

c) The elevator come to stop and then start accelerating downward at 3 m/s^2. What is the reading on the scale now?

     F = ma = 75 (3) = 225 N

     Fnet = 735 - 225 = 510N

     

Newton's First Law of Motion

Newton's Laws of Motion

• Provide the foundation for all the root of physics
• There are 3 fundamental laws of motion

Newton's  first law:

• Also called the law of Inertia
• "A body at rest will stay at rest. If in motion will remain in motion unless acted upon by an unbalanced external force."
• In space where there is no friction, a body will continue to move indefinitely if it is already in motion.

 Inertia

• The resistance that a body demonstrates to a change in its state of motion.
• All object have inertia. 
• The amount of inertia possessed by a body is determined by its mass.  (Remember that mass is the amount of matter contained within an object)

Example: If a 150 lbs person run into a 150 lbs person, he could able to stop. If a 300 lbs person run into a 150 lbs person, he could not be able to stop.

• The more mass an object has, the greater its inertia. In other word, the harder it is to move it or slow it down.

Balanced vs Unbalanced forces: If a forces acts on a body, and there is no force to counter it, the force is said to be unbalanced.

• First box - Unbalanced force of 50 Newtons applied to the box
• Second box - The force are balanced. That is, they canceled out.

Graphical Analysis of Motion

Graphical Analysis of Motion

     Distance vs Time or Displacement vs Time or Position vs Time

• The slope always represent the speed on a distance vs time graph.
• High slope = faster speed
• Low slope = slower speed
• A straight line  means constant speed
• slope = rise/ run = 5/2 = 2.5 m/s = constant speed
• slope = 5 m/ 2 s = 2.5 m/s

Example: 

     If a rock is dropped from a high cliff. The rock fall for 5 sec, how far did it traveled?

     

d = si*t + (1/2)a t^2     si = 0 (initial speed)    t = 5s    a = 9.8 m/s^2

d1 = 1/2 (9.8) (1s)^2 = 4.9 m

d2 = 1/2 (9.8) (2s)^2 = 19.6 m

d3 = 1/2 (9.8) (3s)^2 = 44.1 m

d4 = 1/2 (9.8) (4s)^2 = 78.4 m

d5 = 1/2 (9.8) (5s)^2 = 122.5 m

    

   

• A constant acceleration will create a curve line (parabola).
• The slope at any given point is the speed or velocity at that instant
• The instantaneous speed is found by drawing a tangent line to any point on the curve line.
• slope = Δd / Δt 

 Speed vs Time graph

• Area below the line on a speed vs time graph is the distance traveled.
• Area = L * W => d = s * t =  3 s * 10 m/s = 30 m

• Straight line means constant acceleration = slope = (6 m/s) / 5 s = 1.2 m/s^2
• Initial speed =0, Distance traveled =>d = (1/2)at^2 = (1/2) (1.2)(5)^2 = 15 m
• Area = 1/2bh = (1/2)(5)(6) = 15 m 

Velocity vs Time graph

• Slope is always = accelerate on a velocity vs time graph
• In this case the slope is negative, so it is decelerate.
• Slope = (0-140)/ (8-0) = - 17.5 m/s^2
• Distance = Area of the line => A = (1/2)bh = (1/2)(8)(140) = 560 m
• Distance = d = si*t + (1/2) at^2 = (140)(8) + (1/2) (-17.5) (8)^2 = 560 m

Acceleration vs Time graph

• Straight line means constant acceleration = 10 m/s^2 , but velocity is changing by the same rate each second
• Area under the line gives the change in velocity during the time interval 5 secs. 

Area = (10 m/s^2 )(5s) = 50 m/s =  Δv (change in velocity)

Formula:

1) d = si*t = (1/2) a*t^2     a = (2d) / t^2

2) d = (sf^2 - si^2) / 2a     a = (sf^2 - si^2) / 2d

3) a = (sf - si) / t     t = (sf -si) / a

    _

4) s = d / t     t = d / s     d = s*t

    _

5) s = (si +sf) /2

6) sf = si + a*t

Kinematics: Study of motion

Includes the concepts of:

• speed
• velocity
• acceleration
• time
• distance
• displacement

Vectors: is a quantity which express both magnitude and direction.

• magnitude is how big or how small a number is
• direction is which way something is headed or directed.
• example; velocity, displacement, force, accerleration

Scalars: is a quantity which express magnitude only 

• no direction is specified
• example; speed, mass, distance, energy

Distance: how far something has traveled

• no direction is specified
• commonly measure in meters, kilometers, and centimeters
• is a scalar

Displacement: how far something is from its starting point

• direction is specified
• is a vector

 

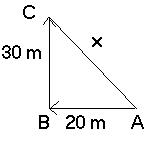
Example: An object travel 20 meters west then 30 meters north.

                  a) What is the distance traveled?

                  b) What is the displacement?

Use Pythagorean Theorem: a^2 +b^2 = c^2

                    

                    a) Distance = 20 m +30 m = 50 m

                    b) Displacement = 20^2 +30^2 = x^2

                                                     √ (1300)   = x^2

                                               36.06 m = x (North West)

Speed: how fast something is traveling

• speed is the distance covered in a given amount of time
• is a scalar

   The formula for speed: s = d/t, s= speed, d = distance, t = time

    

Example 1) An object covered a distance of 75 kilometers in half an hour. What is the speed in a) kilometers/hour b) meters/second

     a) s = d/t = 75 kilometers / .5 h = 150 km/h

    

    b) (150 km)/ h * (1000 m)/ km * h/(3600 s) = 41.67 m/s 

Example 2) An object covered 450 m in 20 s. What is it speed in a) m/s b) km/h?

     a) s= d/t = 450 m/20 s = 22.5 m/s

     

     b) (22.5 m)/ s * km/ (1000 m) (3600 s)/h) = 81 km/h

Example 3) A rifle fire a bullet at a target. The speed of the bullet is 700 m/s. The target is located 250 meters away.

     a) How long does it take for the bullet to hit the target?

    b) What is the bullet speed in km/h?

     a) s = d/t => 700 m/s  = (250 m)/ t => 250 m*(1s/700 m) = (t/250m) *250 m => 250/700 = t, t = .35 secs.

   b) (700 m)/ s * (3600 s)/h * km/ (1000 m) = 2520 km/h

Velocity: how fast something is traveling and in what direction

• is a vector

Example:

     a)  An object travel 45 m/s is a speed

     b)  An object travel 45 ms due south is a velocity

Acceleration: how fast speed or velocity changes

• the rate at which speed or velocity changes
• if an object speed up, it has a positive acceleration
• if an object slowing down, it has a negative acceleration

The formula to calculate the acceleration is: a =  Δ's / t

• Δ's is the change in speed, Δ is Delta
• t is the time
• the change in speed is calculate using sf - si
• sf = the final speed
• si = the initial speed
• therefore a= (sf - si)/ t

Examples 1) A new Nissan GT-R 35, Spec V acceleration from 0 mph to 60 mph in 3.2 secs. What is it rate of acceleration?

     a = (sf - si) /t = (60 - 0) / 3.2 = 18.75 (m/h)/s, mph = miles per hour. So in 1 sec, the car go 18.75 miles per hour.

Example 2) A car goes from 20 m/s to 50 m/s in 10 s. What is the rate of acceleration?

     a = (sf - si) /t = (50-20)/ 10 = 3 m/s^2 

         (m/s) /s => m/s x 1/s = m/s^2

The average speed of a uniformly acceleration object:

Example:  If a car goes from 10 m/s to 30 m/s in 3 s.

     a) What is its acceleration rate?

        

         a = (sf - si)/t = (30 - 10) / 3 = 6.67 m/s^2

     b) What is it average speed over the 3 s interval?

                                                                        -

         The formula to calculate average speed: s = (si + sf) /2

= (10 + 30) / 2 = 40/2 = 20 m/s

Rearranging acceleration formula: a = (sf - si) /t 

• First multiply both side by t => a*t = sf - si
• Final speed of an object base on initial speed, acceleration and time. => sf = si +a*t

Example 1) An airplane traveling at 300 m/s accelerates uniformly at the rate of 12 m/s^2. What its speed be at the end of 30 secs?

     si = 3000 m/s     a = 120 m/s^2     t = 30 s     sf = ?

   sf = si + at = 300 m/s + (120 m/s^2) (30 s) 

                     = 300 m/s + 360 m/s = 660 m/s

Example 2) An automobile accelerate at the rate of 7.5 m/s^2. It goes from 15 m/s to 85 m/s. While it is accelerating, how long did it take to reach 85 m/s ?

     

     a = 7.5 m/s^2     si = 15 m/s     sf = 85 m/s     t = ?

     sf = si + at => 85 m/s = 15 m/s + (7.5 m/s^2) t

                             70 = 7.5 t, t =9.33 s

Distance based on si, a, and t: To calculate how far 
an object travels 

based on initial speed, acceleration rate, and time.

The following equation is used => d = si*t + (1/2) a t^2

• d = distance traveled
• si = initial speed
• a = acceleration rate
• t = time

Example 1) A rocket is accelerate from 300 m/s at 
the rate of 9.5 m/s^2 for 20 sec. 

     

     a)What is the rocket final speed?

     

          si = 300 m/s     a = 9.5 m/s^2     t = 20s

          

          sf = si + at = 300 m/s + 9.5 m/s^2 (20s)

                            = 300 m/s + 190 m/s = 490 m/s

     b) What is the distance traveled by the rocket during the 20 sec?

          d = si*t + (1/2) a t^2 = 300 m/s (20s) = (1/2)(9.5 m/s^2)(20s)^2

                                           = 6000 m + 1900 m  = 7900 m

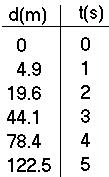
Example 2) A rock is dropped off a bridge. Gravity 
accelerates falling objects at the rate of  9.8 m/s^2.

     a) If the rock fall for 5 sec, how far did it traveled?

          si = 0     a = 9.8 m/s^2     t= 5s

          d = (0) (5s) + (1/2)(9.8 m/s^2) (5s)^2

         

             =    0        + (9.8 x 25)/2 = 122.5 m

     b) How fast was it going at the end of 5 secs?   

          sf = si + at = 0 + (9.8 m/s^2) 5s =  49 m/s 

The last kinematics formula: 

     a = (sf^2 - si^2) / 2d          d = (sf^2 - si^2) / 2a

• sf = final speed
• si = initial speed
• d = distance traveled
• a = acceleration rate

Example 1) A supersonic jet travelling at 400 m/s accelerate to 750 m/s at a rate of 18 m/s^2. What distance does it cover during this time?

     si = 400 m/s     sf = 750 m/s      a = 18 m/s^2

     d = [(750 m/s) ^2 - (400 m/s)^2] / 2 (18 m/s^2) = 11, 180.55 m

Example 2) A race car travels 800 m while acceleration at the rate of 5 m/s^2. If its initials speed was 30 m/s. What was it final speed?

     sf = si + at     a = (sf^2 - si^2)/ 2d

     5 m/s^2 = [sf^2 - (30 m/s)^2 ] / 2 (800 m)

     1600 (5) = [(sf^2 - 900)/ 1600] (1600)

      8000 + 900  = sf^2 -900 +900

   

           8900       = sf^2

          

           √8900     = sf^2

     

          94.34 m/s = sf 

Trigonometric Functions

Trigonometric Functions

a) right triangles , triangles that contain a 90° angle.

b) adjacent side always makes up of θ (Theta) and the hypotenuse side

Example:

            1)

                 Tangent 42° = O / A = x / 25 m 

     

                           25 (.9004) = (x / 25) (25)

                              22.51 m =  x

             2)

                                

                              Sine 35° = O / H = x / 18 m

                    18(.5736) = (x / 18)(18)

                   10.3248 m = x

                     

Scientific Notation

Scientific Notation

A way of expressing very large  or very small number using power of 10.

     coefficient = a, base = 10, exponent = b

Write a number in scientific notation:

Example: 

1) 125,000,000,000

     a) Put a decimal after the first digit and drop the zeros; 1.25 will be the coefficient

     b) To find the exponent, count the places from the decimal to the end of the number; 11 is the exponent

     c) So, the scientific notation is 1.25 x 10 ^11

2) 0.000000000000244  = 2.44 x 10^-13 

(Numbers smaller than 1 will have a negative exponent)

3) 360,000,000,000,000  = 3.6 x 10^14

4) 0.000000297              = 2.97 x 10^-7

5) 125,000,000               = 1.25 x 10^8

6) 1,380,000                   = 1.38 x 10^6

7) .000,006                     = 6.0 x 10^-6

8) .0000274                    = 2.74 x 10^-5

Adding and Subtract using Scientific Notation:

Examples:

     1)   3.6 x 10^5             2)       8.4 x 10^8

          +                                     -

           4.5 x 10^5                       3.2 x 10^8

           -------------                      -------------

           8.1 x 10^5                       5.2 x 10^8

     3)   4.5 x 10^6        =>         0.45 x 10^7

          +                          

           2.2 x 10^7                      2.2   x 10^7

                                     ^           --------------

                                     ||           2.65 x 10^7

                                     ||

          a) increase the smaller exponent to equal the larger exponent

          b) decrease the size of corresponding coefficient amount

     4)   3.3 x 10^9                      3.3   x 10^9

          +                       =>       +

           2.2 x 10^8                      0.22 x 10^9

                                                  --------------

                                                  3.52 x 10^9

     5)   8.4 x 10^5                      8.40  x 10^5

          -                       =>        -

           3.4 x 10^4                      0.34  x 10^5

                                                  -------------

                                                  8.06  x 10^5

    6)    3.3 x 10^-7                     3.30 x 10^-7

          +                     =>           + 

           8.6 x 10^-8                     0.86 x 10^-7

                                                  ---------------

                                                  4.16 x 10^-7

    7)    3.6 x 10^-9                     3.60 x 10^-9

          -                     =>           -

           4.4 x 10^-10                   0.44 x 10^-9

                                                 ----------------

                                                  3.16 x 10^-9

Multiply and Divide using Scientific Notation: 

 A) When multiply, multiple the coefficients with the powers of ten, you add the exponent.

(a x 10^b) * (c x 10^d) = (a*c) x 10^(b +d)

Example 1: 

(5.2 x 10^2) * (2.5 x 10^3) = (5.2*2.5) x 10^(2+3) = 13 x 10^5  (Proper scientific notation is 1.3 x 10^6)

B) When divide, divide the coefficient with the powers of ten, you subtract the exponent.

(a x 10^b) / (c x 10^d) = (a/c) x 10^(b-d)

Example 1: 

(6.3 x 10^4) / (2.1 x 10^2) = 6.3/2.1 x 10^(4-2) = 3 x 10^2

Example 2: 

(8.49 x 10^-6) / (3.0 x 10^-3) = (8.49/3.0) x 10^(-6-( -3)) = 2.83 x 10^ -3 (Negative exponent!)

Example 3: 

(8 x 10^3) (2 x 10^2)        

-------------------------   =   [(8)(2)] /4  x 10^[ (3+2)-3]  =  4 x 10^2

      (4 x 10^3)                      

                                                        

Scientific Method

(Then...)

Scientific Method

A systematic procedure for solving problem in science.

The steps in the scientific method:

1. Problem Statement
2. Research
3. Hypothesis
4. Procedure
5. Data and Observations
6. Conclusion

There are also theories and laws.

1. Problem Statement: What are you trying to accomplish in the experiment.

2. Research: Find out about the topic, gather information and references related to the problem.

3. Hypothesis: An educated guess as to what you think will happen in an experiment.

    

     Example: I believe that the dog will be flattened. (When a heavy weight dropped on it).

3. Procedure: The steps that you will follow in executing the experiment.

4. Data and Observation: What you observe in an experiment. Includes all pertinent characteristic and measurement.

5. Conclusion: A statement of what happened and whether or not this agrees with your hypothesis.

    Example: My hypothesis was correct. The dog got flattened.

6. Theory: An explanation for what happened in the experiment.

7. Law: A scientific fact that has withstand the test of time and repeated experimentation.

     Example: Law of gravity - All object are attracted toward the center of the Earth.

Metric System

Metric System Prefixes

Metric System

Based on multiples of 10. Prefixed are place in front of the base unit to represent larger or smaller quantities.

Important prefixes:

     kilo (K)      = 1,000
     hecto (H)   = 100
     deca (D)   = 10
     Base         = 1 (meter, gram, liter, joule)
     deci (d)     = .1 (1/10)
     centi (c)    = .01 (1/100)
     milli (m)    = .001 (1/1,000)

Other prefixes:
     mega (M)  = 1000,000
     giga (G)     = 100,0000,000
     micro (µ)   = 1/1000,000

Base Units:

• meter (m) is the base unit for length
• gram (g)     "        mass
• liter (l)        "       volume
• joule (J)      "       energy

Examples:

   1) Convert 30 mL to kL

         a) 30.0, move the decimal to the left six places,  = .000030 kL

          OR 

         b)

    2) How many grams are there in 5 kilogram (kg) ?

         a) 5.0, move the decimal to the right three places, = 5000. g

OR

         b)

    3) Convert 350 Dg to mg.

          a) 350.0, move the decimal to the right four places, = 3500000. mg

          OR

          b)

      4) Convert 20 cm to m.

          a) 20.0, move the decimal to the left two places, = .20 m

          OR

          b) 

Measurement of matter

     Mass: the amount of matter within an object
     
     Weight: the force of gravity of mater acting on an object (9.8 m/s^2)

     Volume: the amount of space taken up by an object.
                  
                   Volume = A x h, A = area, h = height